一、题目

　　1、审题

　　2、分析

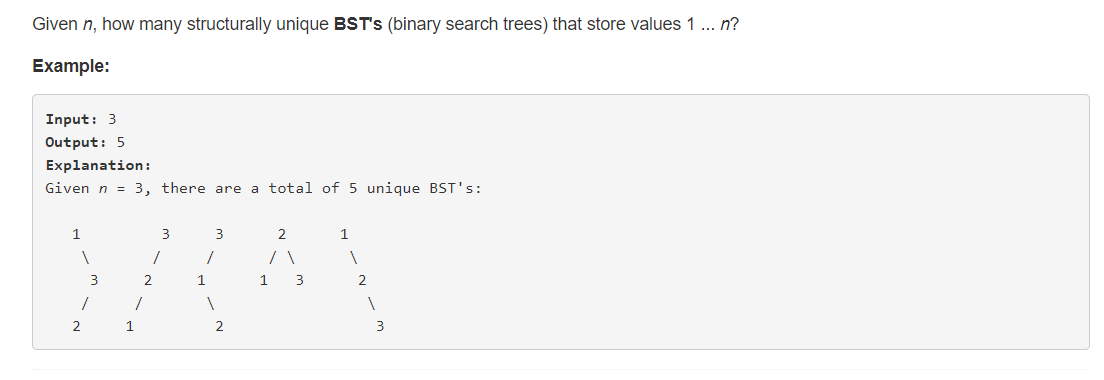
　　　　给出整数 n ，求 n 个节点能组成多少个不同的二分查找数。

 

二、解答

　　1、思路：

　　　　（引自： https://leetcode.com/problems/unique-binary-search-trees/discuss/31666/DP-Solution-in-6-lines-with-explanation.-F(i-n)-G(i-1)-*-G(n-i)）

　　　　　　定义两个方法，G(n), F(i, n),

　　　　　　①、G（n）表示 n 个节点时共有多少种二分查找树。

　　　　　　②、 F(i, n) 表示 n 个节点时 i 为顶点，则左子树含有 i-1个节点，排序数记作G(i-1)，右子树含有 n - i 个节点 ，排序数记作 G(n-i)。

　　　　　　③、G(n) = F(1,n) + F(2,n) + ... + F(n, n)

　　　　　　　　　　 = G(0)*G(n-1) + G(1)*G(n-2) + ... + G(n-1)*G(0);

　　　　　　④、G(1) 代表只有一个节点时的二叉查找树个数，为 1；

　　　　　　　　G(0) 为了满足 ③ 中的计算，即 F(n,n) = G(n-1)*G(0) = G(n-1)；故 G(0) = 1;

　　　　所以，要求的即为 G(n)；

public int numTrees(int n) {                int[] G = new int[n+1];        G[0] = 1;        G[1] = 1;        for (int i = 2; i <= n; i++) {        // 节点数            for (int j = 1; j <= i; j++) {    // 顶点                G[i] += G[j-1]*G[i-j];            }        }        return G[n];    }